4469. Домино

Найдите количество способов покрытия прямоугольника 2 × n прямоугольниками 2 × 1. Покрытия, которые превращаются сами в себя симметриями считать разными.

Вход. Одно число n (0 < n < 65536).

Выход. Вывести искомое количество способов.

Пример входа 1	Пример выхода 1
1	1
Пример входа 2	Пример выхода 2
4	5

РЕШЕНИЕ

числа Фибоначчи

Анализ алгоритма

Обозначим через f(n) количество способов, которыми можно покрыть прямоугольник 2 × n костями домино 2 × 1. Очевидно, что

· f(1) = 1, одна вертикальная кость;

· f(2) = 2, две вертикальные или две горизонтальные кости.

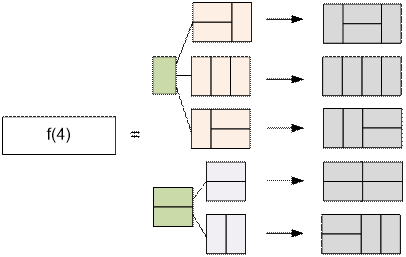
Рассмотрим алгоритм вычисления f(n). Можно положить одну кость вертикально и далее покрывать прямоугольник длины n – 1 f(n – 1) способом, или положить две кости горизонтально и далее покрывать прямоугольник длины n – 2 f(n – 2) способами. То есть f(n) = f(n – 1) + f(n – 2).

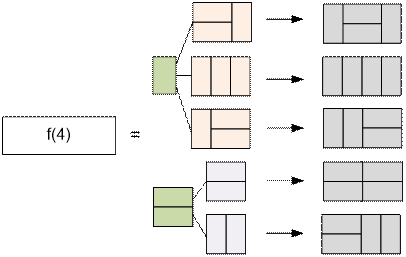
Таким образом, f(n) является числом Фибоначчи.

Реализация алгоритма

Поскольку n < 65536, то следует воспользоваться длинной арифметикой или языком программирования Java.

import java.util.*;

import java.math.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

BigInteger a = new BigInteger("1"), b = a;

for(int i = 0; i < n; i++)

{

BigInteger temp = a.add(b);

a = b;

b = temp;

}

System.out.println(a);

con.close();

}

}